Code Implementation
To download, install, and run the BEHALF package, see the Github Source Repository.
Octree
There are two main algorithms required for the force calculation using an octree: (1) building the tree and (2) traversing the tree to calculate the force on a single body. The pseudocode for these two algorithms is presented below.
function insertParticle(particle, node)
if(particle.position is not in node.box): # if particle is not in node's
bounding box return # end function if(node has no particles):
node.particle = particle #
particle is now assigned to node if(node is an internal node):
updateCenterOfMass(node) # update center of mass of node
updateTotalMass(node) # update total mass of node for child
in node.children: insertParticle(particle, child) # insert particle
into the appropriate child node if(node is an external node): # if node already has another particle
associated with it createChildren(node) # subdivide this node into its 8 children for child
in node.children:
insertParticle(node.particle, child) # insert the existing
node.particle into the appropriate child node for child in node.children:
insertParticle(particle, child) # insert particle into the appropriate child node
The insertParticle algorithm must be run for every particle in the simulation. The algorithm starts by checking to see if the particle is inside the given node's bounding box. Assuming it is, if the node has no particles, the particle currently being considered will be assigned to the given node. If the node is an internal node (that is, it has child nodes) but has no particles associated with it, we insert the particle into the appropriate child node and update the center of mass and the total mass of the node. If the node is an external node (i.e. it has no children) but already has a particle associated with it, we must first create children for that node and then recursively assign both the particle that was already assigned to the external node and the new particle that we were originally assigning. Once we loop over all particles, each leaf node will have only one particle associated with it.
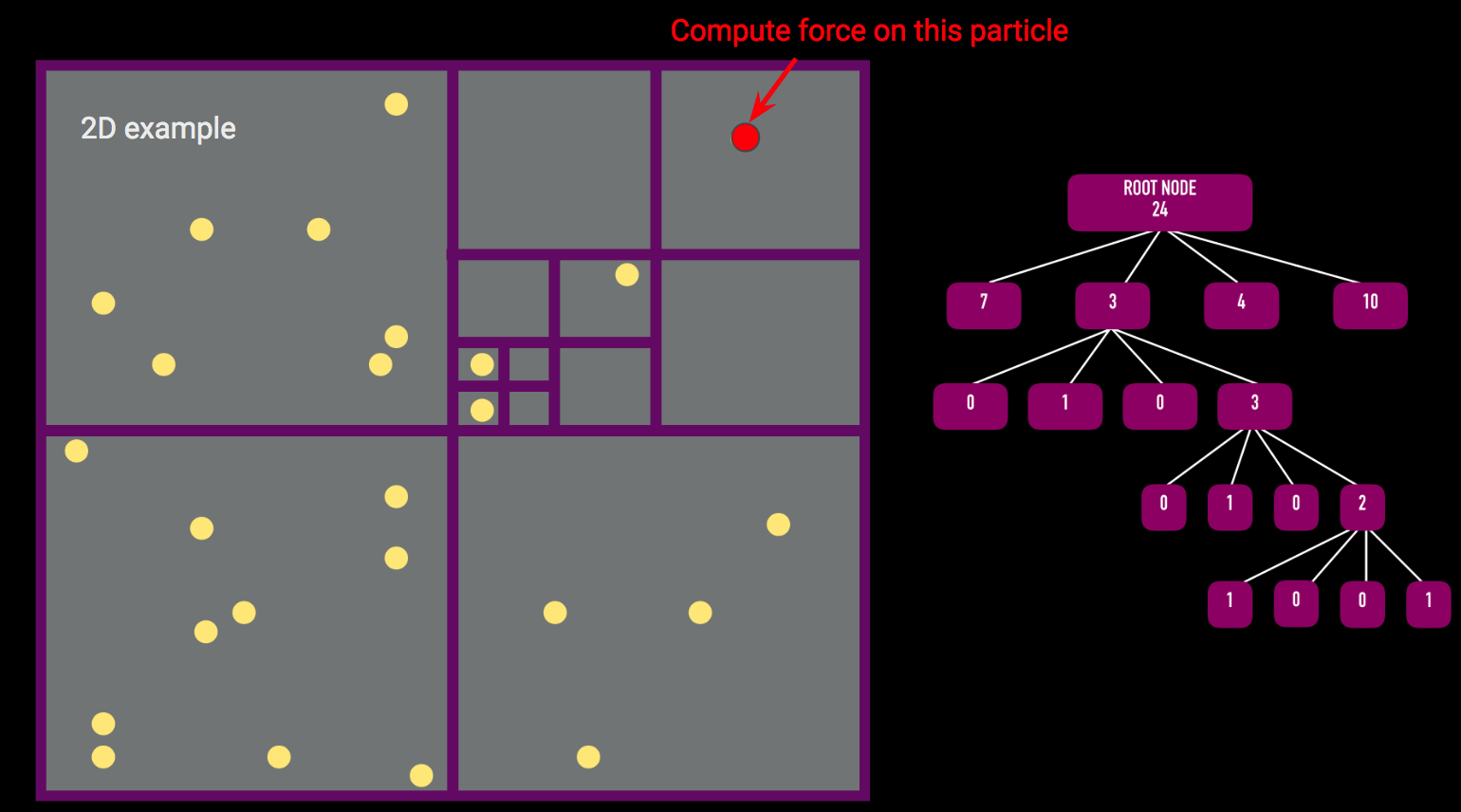
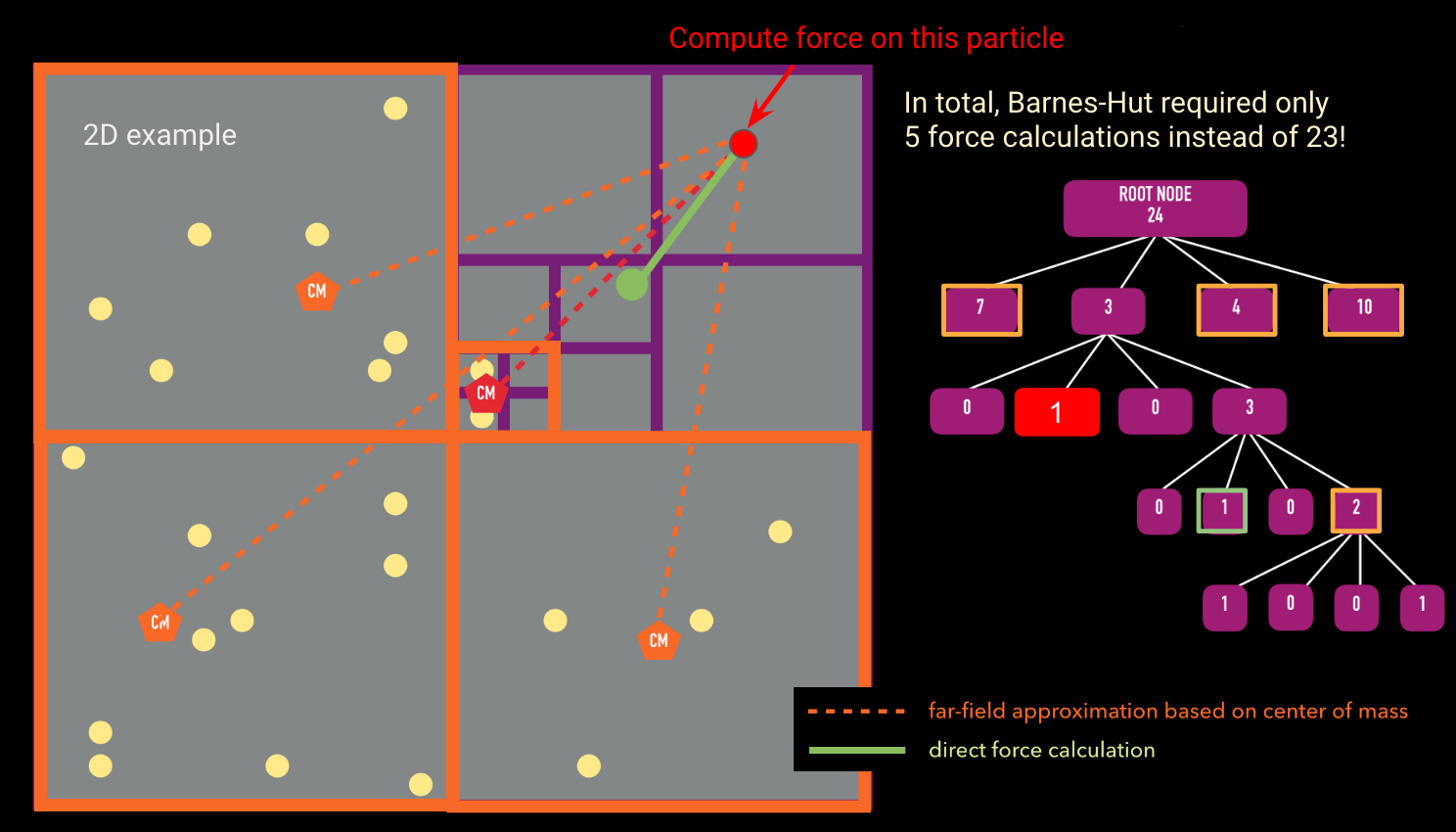
function calculateAcceleration(particle, node, thetaTolerance)
if(node.leaf):
directAccelCalculation(node.particle, particle) # directly sum this node's
particle's force on the particle we're considering theta
= node.size/distance(node.com, particle.position)
if(theta is less than thetaTolerance):
farFieldForceCalculation(node.mass, node.com, particle)
# far field approximation is valid else: # far field approximation is not valid for child in node.chilren:
calculateAcceleration(particle, child, thetaTolerance)
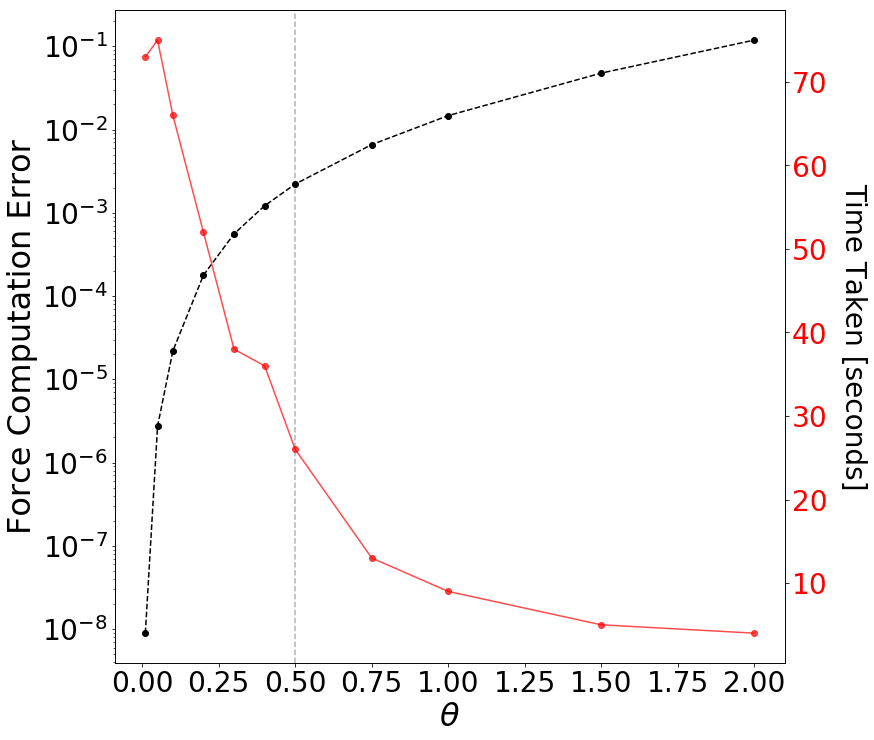
calculateAcceleration takes in the particle we want to calculate the force for, the node we are currently comparing against, and thetaTolerance (the opening angle). The algorithm first starts by checking whether the node we are currently comparing against is a leaf node. If it is, it holds only one particle and we must directly calculate the gravitational influence of this particle on the the particle we passed in as an argument. If the current node is not a leaf, we calculate the opening angle theta (given by the size of the node divided by the distance from the node to the particle). If the opening angle is less than some pre-defined thetaTolerance (most codes in literature use 0.5; Springel et al. 2005 ), the far field approximation is valid and we can group all the particles belonging to this node and compute the gravitational influence of this group on the particle we want to calculate the acceleration for. If the far field approximation is not valid, we must open up the node and call calculateAcceleration for all children of the original node.
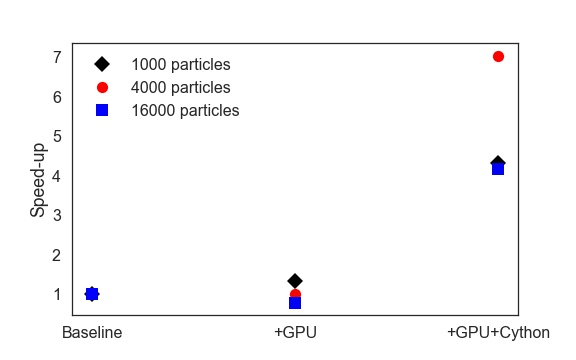
Through experimentation, we found that there was a significant amount of overhead associated with the original Python version of calculateAcceleration. Therefore, we optimized the force calculation using Cython. The speed-ups with the Cython version are shown in the Advanced Features section.
Leapfrog Algorithm
Once the forces are calculated, we use
the Leapfrog
Algorithm to update the positions and velocities. The Leapfrog integration
algorithm is a symplectic (i.e. time-reversible) method for solving the set of
differential equations given by Newton's laws:
\(v = \frac{dx}{dt}\)
\(F = m \frac{d^2x}{dt^2}\)
Because it is symplectic, the Leapfrog Algorithm is guaranteed to conserve energy
(to reasonable precision, determined by the time step chosen). Even though it is a
first-order integrator, it performs better than higher-order algorithms (like 4th
order Runge-Kutta) at conserving energy over many time steps.
The algorithm is nearly identical to the Euler method, except the velocities and
positions are computed at half-timestep offsets:
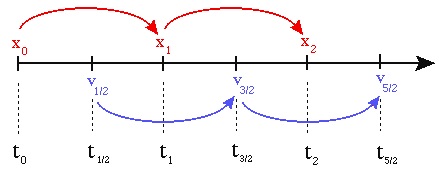 Therefore, there is an initial self-start phase of a half-step:
Therefore, there is an initial self-start phase of a half-step:
\(a_0 = F(x_0) /
m \)
\(v_{\frac{1}{2}} = v_0 + a_0 \frac{dt}{2} \)
\(x_1 = x_0 +
v_{\frac{1}{2}} dt\)
followed by the regular Euler updating kick-drift
steps:
\(a_1 = F(x_1) / m \)
\(v_{\frac{3}{2}} = v_{\frac{1}{2}} + a_1
dt\)
\(x_2 = x_1 + v_{\frac{3}{2}} dt\)
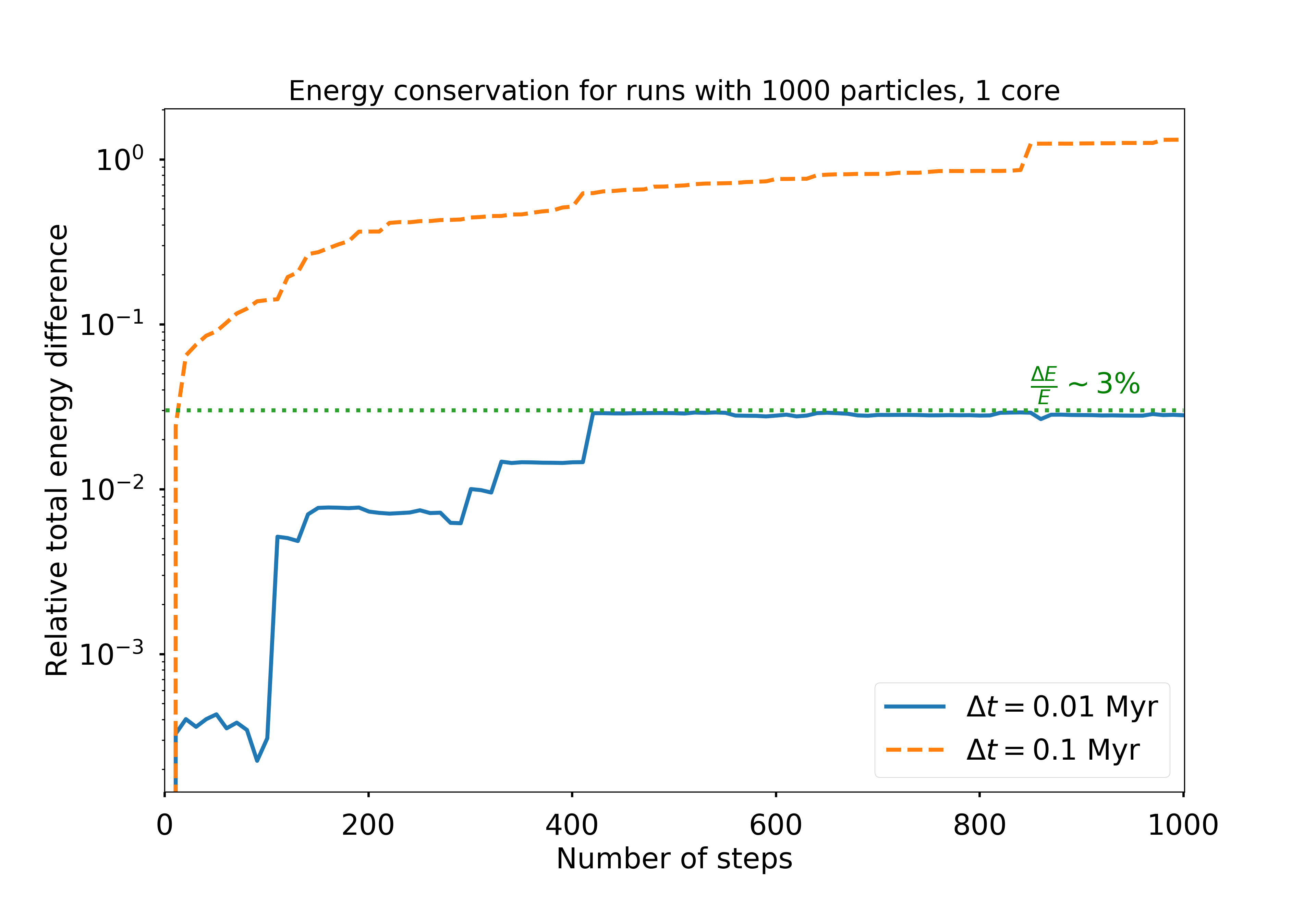
We discuss the choice of timestep that results in acceptable levels of energy
error below.
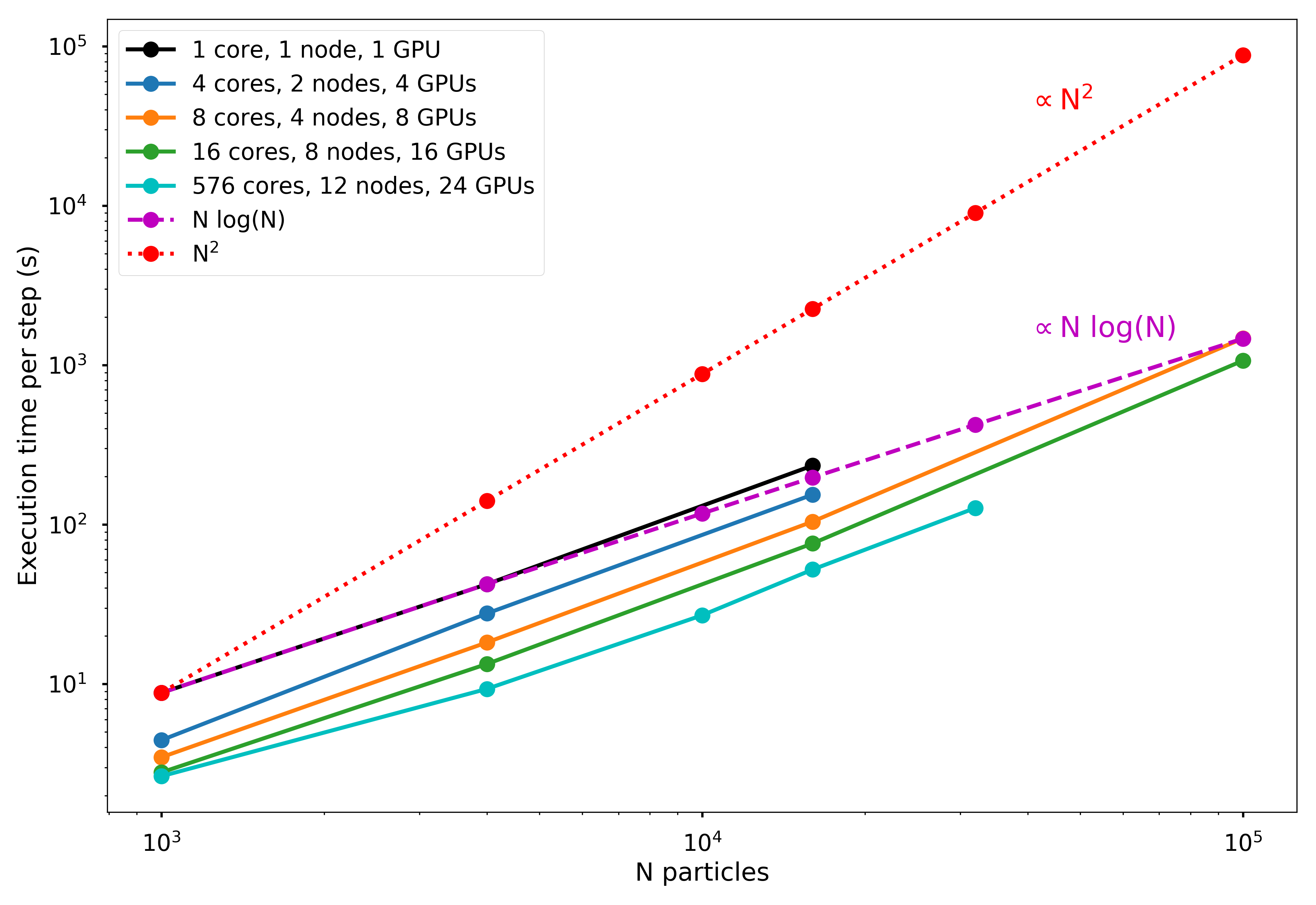
Parallel Algorithm
Each step of the N-body integration algorithm has the following structure:
- Build the Octree
- For each particle: compute the total force by traversing the Octree
- Update the velocities and positions using LeapFrog time integration algorithm
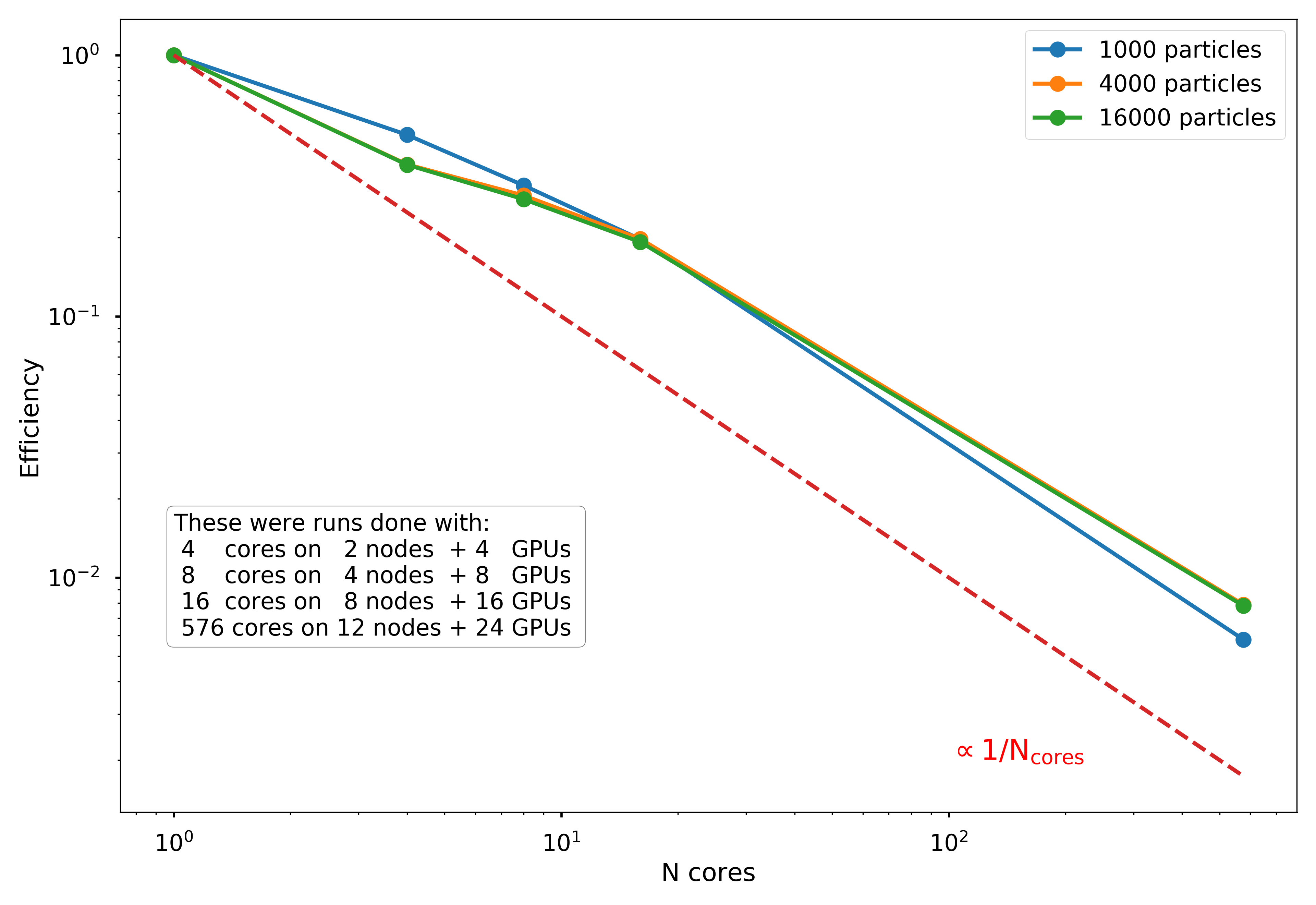
For step (2), once the tree is created, we use MPI to broadcast the entire tree to a system of distributed-memory processes. The simulated particles are then distributed nearly exactly evenly (to within \(\pm 1\) particle) across the processes, and the force calculation occurs in parallel. As discussed below, the force calculation is initially one of the most computationally demanding portions of the code, but this is conveniently the most trivially parallelizable portion, as distributing particles onto more processes nearly linearly reduces the execution time.
The second phase of parallelization comes in step (3), as we implemented the time integration step on GPUs using PyCUDA. The velocity and positions are updated for each particle in parallel on the GPU processors, which theoretically should provide significant speed-up. However, there are non-trivial overheads involved in moving to GPU acceleration. For one, the communication overhead of sending data to/from the GPU over the PCI-e bus can be significant, and speed-ups over basic Python implementation may not be seen unless a very large number of particles is used.
In addition, the number of GPUs available on a given node is typically much smaller (around 2, when available at all) than the number of CPUs. This means that for a fixed number of nodes, there may be as many as 32 times more CPUs available than GPUs. If all CPUs are being used to distribute MPI processes, then many processes will need to bind to the same GPUs, which limits the overall scalability of the GPU algorithm. In the sections below we examine these potential limitations, ultimately finding that the GPU acceleration of the time integration step does not significantly improve the execution time in our tests, likely because too few particles were used to overcome the overheads.
Including the communication overheads, the final parallel algorithm has the following steps:
- Build the Octree (on primary MPI node)
- Octree is broadcast to all MPI nodes
- For each particle: compute the total force by traversing the Octree
- Particle positions and velocities are distributed across MPI nodes
- Update the velocities and positions using LeapFrog time integration algorithm (on the GPU)
- Particle positions, velocities, and accelerations are transferred to the GPU
- Updated particle data retrieved from GPU
- Entire particle catalogs are sent back to the primary MPI node
Advanced Features
We found that a pure Python implementation of the force calculation came with many overheads due to looping in Python. Instead, we wrote a Cython version of the force calculation and traversal to mitigate this. We found that, on average, the Cython version performed three times faster than the pure Python version. As discussed later, however, the GPU acceleration was fairly insignificant, or even detrimental, as the communication overhead was simply too large for this relatively small simulation size.
Infrastructure
The BEHALF package was developed and tested in Python 3.6 (but backported to support 2.7). Serial jobs without GPU acceleration were tested on Harvard's Odyssey cluster, on a private research queue. Each core on the queue has a CPU clock of 2.3 GHz and operates on CentOS release 6.5.
The primary testing runs were performed on the holyseasgpu queue. Each of the 12 available nodes on this queue have 48 cores, a CPU clock of 2.4 GHz, and 2 NVIDIA Tesla K40m GPUs, operating on CUDA 7.5.
The BEHALF package was tested with the following Python package versions:
- numpy: v1.12.1
- pycuda: v2017.1.1
- mpi4py: v2.0.0
- future: v0.16.0
- cython: v0.26
For details on the installation requirements and dependencies, see the Github Source Repository.




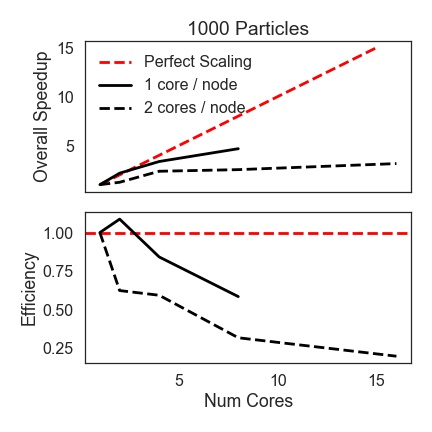
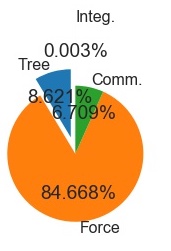 1000 Particle Serial Run (+GPU
+Cython)
1000 Particle Serial Run (+GPU
+Cython)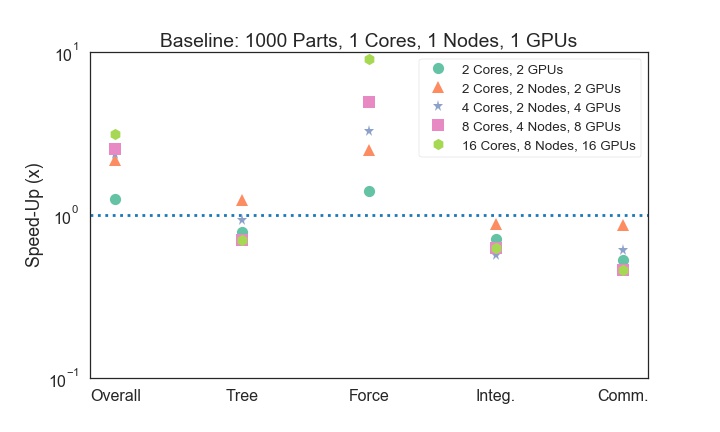
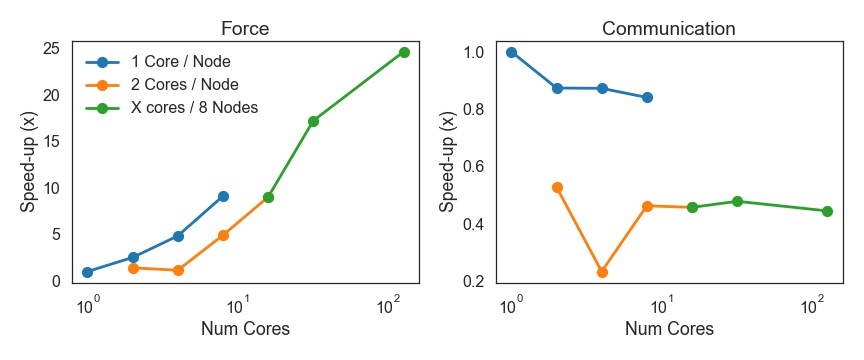
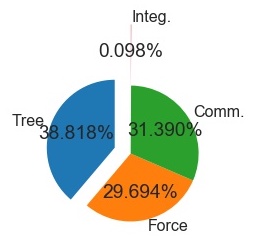 1000 Particle Run, 16
cores, 8 nodes(+GPU
+Cython)
1000 Particle Run, 16
cores, 8 nodes(+GPU
+Cython)